Il paradosso di San Pietroburgo è un gioco teorico utilizzato in economia per mostrare un tipico esempio in cui il decisore è indotto in errore a prendere una decisione irragionevole considerando solo il valore atteso come unico criterio decisionale.
Questo enigma fu proposto e risolto per la prima volta nel “Commentarii Academiae Scientiarum Imperialis Petropolitanae” di Daniel Bernoulli (tradotto come “Esposizione di una nuova teoria sulla misurazione del rischio”) nel 1738, dando origine al nome della città, San Pietroburgo.

Bernoulli ha risolto il problema distinguendo tra valore atteso e utilità attesa, poiché quest’ultimo utilizza l’utilità ponderata moltiplicata per la probabilità piuttosto che i risultati ponderati. Tuttavia, da allora molti ricercatori hanno utilizzato tecniche alternative per rispondere a questo dilemma.
Table of Contents
Il paradosso di San Pietroburgo
La chiave per risolvere l’enigma è determinare quanto qualcuno sarebbe disposto a pagare per giocare a una lotteria che funziona come segue:
- Viene lanciata una moneta non truccata
- se appare la croce, al giocatore vengono assegnati $2 (supponendo che l’importo pagato per giocare sia $1)
- Se la croce non si vede, la moneta viene lanciata di nuovo, raddoppiando il guadagno iniziale ogni volta che la moneta viene lanciata.
Per il lancio numero 3 (n=3), ad esempio, la vincita sarebbe 8 (2n) e il valore atteso, che equivale alla vincita moltiplicata per la possibilità. (Vedi immagine seguente)
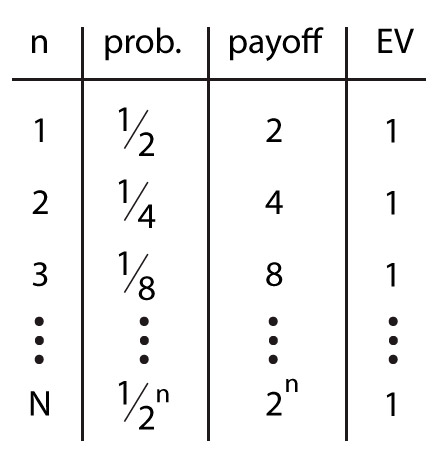
La probabilità di vedere la prima croce nel lancio numero n è pari a pn=1/2n, dove 2n è la ricompensa. Di conseguenza, il valore atteso per n lanci è:
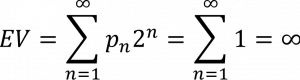
Se il valore atteso viene utilizzato come unico criterio decisionale, il giocatore dovrebbe essere disposto a spendere dollari infiniti per partecipare. Nessuna persona ragionevole, tuttavia, lo accetterebbe. La soluzione di Bernoulli era quella di utilizzare la massima utilità attesa piuttosto che il massimo valore atteso:
![]()
Inoltre, Bernoulli ha affermato che l’utilità aumenta con la ricchezza del giocatore (poiché ha più soldi con cui giocare), mentre l’utilità marginale diminuisce.
Le rivisitazioni successive: Pareto e Marshall
Sebbene semplice e breve, la risposta di Bernoulli al problema di San Pietroburgo fu in seguito ampiamente dibattuta e criticata da altri economisti. Francis Y. Edgeworth ha criticato la sua funzione di utilità logaritmica, utilizzata da Knut Wicksell per sviluppare confronti interpersonali. Nel suo studio sull’enigma, Vilfredo Pareto ha sostituito la ricchezza con il consumo e Alfred Marshall con il reddito.
L’approccio di Alfred Marshall, presentato nel suo libro “Principles of Economics” nel 1890, è di enorme importanza poiché cambia le implicazioni chiave e la soluzione del paradosso semplicemente cambiando la ricchezza con il reddito. Marshall dimostra come, nell’ipotesi di un’utilità marginale decrescente, nessun individuo ragionevole starebbe al gioco perché le perdite supererebbero i vantaggi.
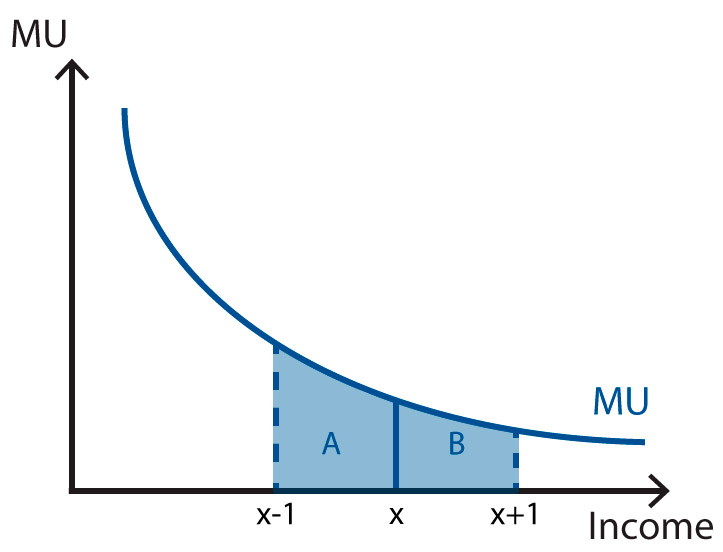
Come indicato nell’immagine qua sotto, supponiamo che la probabilità di vincere la partita sia uguale alla probabilità di perdere, risultando in 12. Se un giocatore perde, perderà l’importo pagato per giocare (x-1); se il giocatore vince, il giocatore vincerà l’importo pagato più uno. Poiché l’area A è più grande dell’area B, nessun giocatore razionale parteciperebbe a causa del declino dell’utilità marginale. Secondo Alfred Marshall:
“L’impiegato che guadagna £100 all’anno andrà a lavorare a piedi sotto una pioggia molto più dura rispetto all’impiegato che guadagna £300 all’anno; poiché il costo di una corsa in tram o in autobus indica un vantaggio maggiore per l’uomo più povero che per il più ricco”. Se l’uomo più povero spende il denaro, soffrirà di più per la sua mancanza rispetto all’uomo ricco. Il vantaggio valutato dalla spesa nella mente dell’uomo più povero è maggiore del beneficio misurato da essa nella mente dell’uomo più ricco.”

Il paradosso di San Pietroburgo ai giorni nostri
La versione originale del dilemma di San Pietroburgo è risolta dall’osservazione di Cramér sull’utilità marginale decrescente del denaro da parte dell’agente. I moderni teorici della decisione, tuttavia, concordano sul fatto che questa soluzione è troppo limitata. Il paradosso può essere rettificato aumentando i valori dei risultati finché l’agente non è completamente compensato per la sua ridotta utilità marginale del denaro (Menger 1934 [1979]). La versione della letteratura moderna del paradosso di San Pietroburgo può quindi essere affermata come segue:
Una moneta non truccata viene lanciata finché non cade sul lato della testa. Il giocatore riceve quindi un premio del valore di unità di utilità sulla scala di utilità personale del giocatore, dove n è il numero di volte in cui la moneta è stata lanciata.
Anche se l’utilità marginale del denaro dell’agente sta diminuendo, l’utilità attesa di questo rischio è illimitata. Possiamo lasciare aperta la questione su quali saranno i premi. Non deve essere monetario.
È importante notare che nessuna delle ricompense nel gioco di San Pietroburgo ha un valore infinito. Il giocatore guadagnerà sempre una quantità finita di utilità, indipendentemente da quante volte la moneta viene lanciata. L’utilità prevista della partita di San Pietroburgo è infinita, mentre il risultato effettivo lo è. Di conseguenza, liquidare il dilemma affermando che nessun premio effettivo può avere un’utilità infinita sarebbe un errore.
James M. Joyce
Alcuni studiosi hanno spiegato perché l’affermazione che l’utilità attesa del gioco di San Pietroburgo modificato sia infinita è dubbia. È semplicemente perché il prezzo ragionevole della scommessa è “troppo alto” o c’è qualcosa di più preoccupante? Secondo James M. Joyce:
Poiché le vincite sono tutte finite, verrà sempre selezionata una scommessa di utilità infinita. Questo è ridicolo, considerando che ci stiamo concentrando sugli scommettitori che vedono le scommesse esclusivamente come un mezzo per espandere la loro fortuna.
(Joyce 1999: 37)
Il punto di Joyce sembra essere che se un agente che paga il giusto prezzo della scommessa, sarà certo che starà peggio dopo aver pagato l’addebito. Tuttavia, questo sembra implicare l’esistenza di veri infiniti. Se ci sono solo infiniti teorici, allora il giocatore non può “pagare” un costo infinito per giocare. Se questo è il caso, Joyce può essere interpretato come se ci ricordasse che non importa quanti soldi il giocatore vince davvero, l’utilità attesa sarà sempre maggiore, il che implica che sarebbe stato logico pagare ancora di più.
I teorici della decisione esaminano una razionalità mezzi-fini, che sostiene che è razionale fare qualunque cosa sia il mezzo migliore per il proprio fine. Di conseguenza, il giocatore comprende che spendere più di una vittoria non può essere il modo migliore per massimizzare l’utilità. Questa intuizione ci permette di rafforzare il “paradosso” iniziale in una versione più robusta composta da tre affermazioni incompatibili:
- La quantità di utilità che si può ottenere giocando al gioco di San Pietroburgo non è finita.
- Il giocatore è consapevole che la quantità di utilità che vincerà è limitata.
- Non è logico pagare di più per una partita di quanto si potrà vincere.
Hajek e Nover
Molti esperti affermano che il valore del gioco di San Pietroburgo è finito per diversi motivi. Hájek e Nover sono una rara eccezione. Ci offrono il seguente esempio per :
Il gioco di San Pietroburgo può essere considerato come il limite di una serie di giochi di San Pietroburgo troncati, con punti di troncamento finiti gradualmente più alti: ad esempio, il gioco viene annullato se non si ottiene testa entro il decimo, undicesimo o dodicesimo lancio; …. Se accettiamo il ragionamento sulla dominanza, questi troncamenti sequenziali possono aiutarci a stimare il valore del gioco di San Pietroburgo: è delimitato in basso da ciascuno dei loro valori, con questi limiti che aumentano in modo monotonicamente. Pertanto, abbiamo una base razionale per accettare che valga la pena spendere qualsiasi somma finita per giocare al gioco di San Pietroburgo. (Hajek e Nover 2006)
Sebbene non lo dichiarino apertamente, è probabile che Hájek e Nover si oppongano. Forse l’affermazione è meno controversa. Naturalmente, è logicamente plausibile che la moneta continui a dare croce ogni volta che viene lanciata, nonostante il fatto che una serie infinita di croce abbia probabilità 0. (Williamson 2007).
Alcuni eventi con probabilità 0 si verificano, ed è impossibile in innumerevoli spazi di probabilità che tutti i risultati abbiano una probabilità maggiore di 0. Anche così, se la moneta restituisce sempre croce, l’agente riceve 0 unità di utilità. Di conseguenza, rimane vero.






